简介
点分治主要解决树上路径问题,其主要思想是把一颗有根树以根为分治点分为一个森林(其实就是各个子树),解决经过当前根的路径后在子树里继续分治,从而将问题“分而治之”。
这里面,根的选择非常重要。为了保证复杂度,我们的分治点应该尽可能的“居中”,所以分治点一般选择正在处理的树的重心。
套路
- 找到当前树的重心作为根
- 解决通过这个根的路径的答案(一般有两种方法,一种是通过与子树容斥,一种是直接计算子树贡献)
- 递归解决子树
实现
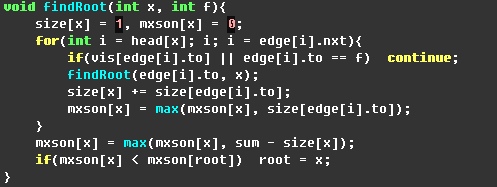
求重心
1 | //root = 0, mxson[0] = INF, sum = n; |
size[]是子树大小,mxson[]是最大子树大小,root是重心,sum是当前整颗树的大小
注意每次 findRoot() 前要初始化 root 和 sum
分治计算
1 | void solve(int x){ |
vis[]标记此点是否计算过,cal()计算以x为根、经过根的路径的答案
注意事项
不要再分治时用memset O(n) 地进行初始化,否则点分治好不容易保证的复杂度就被毁了。
练习
poj1741 tree
题意
给一棵树,边有边权,问两点之间的距离小于等于K的点对有多少个。
题解
点分治时用容斥做:计算以x为根的子树时直接将求得的dis排序后O(n)求答案,然后再减去每个子树中被统计了的不合法答案
Code1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
using namespace std;
const int INF = 1e9;
const int N = 10005;
int n, k, u, v, p;
struct Edge{
int nxt, to, dis;
}edge[N<<1];
int head[N], edgeNum;
void addEdge(int from, int to, int dis){
edge[++edgeNum].nxt = head[from];
edge[edgeNum].to = to;
edge[edgeNum].dis = dis;
head[from] = edgeNum;
}
bool vis[N];
int root, sum, size[N], mxson[N];
void findRoot(int x, int f){
size[x] = 1, mxson[x] = 0;
for(int i = head[x]; i; i = edge[i].nxt){
if(edge[i].to == f || vis[edge[i].to]) continue;
findRoot(edge[i].to, x);
size[x] += size[edge[i].to];
mxson[x] = max(mxson[x], size[edge[i].to]);
}
mxson[x] = max(mxson[x], sum - size[x]);
if(mxson[x] < mxson[root]) root = x;
}
int dis[N], ans;
void getDis(int x, int f, int d){
dis[++dis[0]] = d;
for(int i = head[x]; i; i = edge[i].nxt){
if(edge[i].to == f || vis[edge[i].to]) continue;
getDis(edge[i].to, x, d + edge[i].dis);
}
}
int cal(int x, int d){
int res = 0;
for(int i = 1; i <= dis[0]; i++) dis[i] = 0;
dis[0] = 0;
getDis(x, 0, d);
sort(dis+1, dis+dis[0]+1);
int l = 1, r = dis[0];
while(l < r){
if(dis[l] + dis[r] <= k) res += r - l, l++;
else r--;
}
return res;
}
void solve(int x){
ans += cal(x, 0);
vis[x] = 1;
for(int i = head[x]; i; i = edge[i].nxt){
if(vis[edge[i].to]) continue;
ans -= cal(edge[i].to, edge[i].dis);
root = 0, mxson[0] = INF, sum = size[edge[i].to];
findRoot(edge[i].to, 0);
solve(root);
}
}
void init(){
memset(edge, 0, sizeof edge);
memset(head, 0, sizeof head);
edgeNum = 0;
root = sum = ans = 0;
memset(size, 0, sizeof size);
memset(mxson, 0, sizeof mxson);
memset(vis, 0, sizeof vis);
}
int main(){
while(1){
scanf("%d%d", &n, &k);
if(n == 0 && k == 0) break;
init();
for(int i = 1; i < n; i++){
scanf("%d%d%d", &u, &v, &p);
addEdge(u, v, p);
addEdge(v, u, p);
}
sum = n, root = 0, mxson[0] = INF;
findRoot(1, 0);
solve(root);
printf("%d\n", ans);
}
return 0;
}
luogu3806 【模板】点分治1
题意
给定一棵有n个点的树,多次询问树上距离为k的点对是否存在。
题解
和上一题差不多,也是容斥,只不过我们把所有k的答案一次性求出来,每次询问O(1)回答。
Code1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
using namespace std;
const int INF = 1e9;
const int N = 10005;
int n, m, k[105], u, v, p;
struct Edge{
int nxt, to, dis;
}edge[N<<1];
int head[N], edgeNum;
void addEdge(int from, int to, int dis){
edge[++edgeNum].nxt = head[from];
edge[edgeNum].to = to;
edge[edgeNum].dis = dis;
head[from] = edgeNum;
}
int size[N], mxson[N], dis[N], root, sum;
bool vis[N];
map<int, int> cnt;
void findRoot(int x, int f){
size[x] = 1, mxson[x] = 0;
for(int i = head[x]; i; i = edge[i].nxt){
if(vis[edge[i].to] || edge[i].to == f) continue;
findRoot(edge[i].to, x);
size[x] += size[edge[i].to];
mxson[x] = max(mxson[x], size[edge[i].to]);
}
mxson[x] = max(mxson[x], sum - size[x]);
if(mxson[x] < mxson[root]) root = x;
}
void getDis(int x, int f, int d){
dis[++dis[0]] = d;
for(int i = head[x]; i; i = edge[i].nxt){
if(edge[i].to == f || vis[edge[i].to]) continue;
getDis(edge[i].to, x, d + edge[i].dis);
}
}
void cal(int x, int d, int fl){
for(int i = 1; i <= dis[0]; i++) dis[i] = 0;
dis[0] = 0;
getDis(x, 0, d);
sort(dis+1, dis+dis[0]+1);
for(int i = 1; i <= dis[0]; i++){
for(int j = 1; j <= m; j++){
if(dis[i] + dis[i] > k[j]) continue;
int l = lower_bound(dis+i, dis+dis[0]+1, k[j]-dis[i]) - dis;
if(dis[l] + dis[i] != k[j]) continue;
int r = upper_bound(dis+i, dis+dis[0]+1, k[j]-dis[i]) - dis;
cnt[k[j]] += (r - l) * fl;
}
}
}
void solve(int x){
cal(x, 0, 1);
vis[x] = 1;
for(int i = head[x]; i; i = edge[i].nxt){
if(vis[edge[i].to]) continue;
cal(edge[i].to, edge[i].dis, -1);
root = 0, sum = size[edge[i].to], mxson[0] = INF;
findRoot(edge[i].to, 0);
solve(root);
}
}
int main(){
scanf("%d%d", &n, &m);
for(int i = 1; i < n; i++){
scanf("%d%d%d", &u, &v, &p);
addEdge(u, v, p);
addEdge(v, u, p);
}
for(int i = 1; i <= m; i++)
scanf("%d", &k[i]);
root = 0, sum = n, mxson[0] = INF;
findRoot(1, 0);
solve(root);
for(int i = 1; i <= m; i++)
puts(cnt[k[i]] > 0 ? "AYE" : "NAY");
return 0;
}
[国家集训队] 聪聪可可
题意
求边权和是3的倍数的点对个数
题解
思路和上面两道题大同小异,而且更简单了:不用对dis排序,只需记录下距当前根dis为0,1,2的点的个数(cnt),则答案就是$cnt[0] * cnt[0] + cnt[1] * cnt[2] * 2$
当然这样做也要容斥
Code1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
using namespace std;
const int N = 20005;
const int INF = 1e9;
int n, u, v, p;
struct Edge{
int nxt, to, dis;
}edge[N<<1];
int head[N], edgeNum;
void addEdge(int from, int to, int dis){
edge[++edgeNum].nxt = head[from];
edge[edgeNum].to = to;
edge[edgeNum].dis = dis;
head[from] = edgeNum;
}
int root, mxson[N], sum, size[N];
bool vis[N];
void findRoot(int x, int f){
size[x] = 1, mxson[x] = 0;
for(int i = head[x]; i; i = edge[i].nxt){
if(vis[edge[i].to] || edge[i].to == f) continue;
findRoot(edge[i].to, x);
size[x] += size[edge[i].to];
mxson[x] = max(mxson[x], size[edge[i].to]);
}
mxson[x] = max(mxson[x], sum - size[x]);
if(mxson[x] < mxson[root]) root = x;
}
int cnt[3];
void getDis(int x, int f, int d){
cnt[d%3]++;
for(int i = head[x]; i; i = edge[i].nxt){
if(vis[edge[i].to] || edge[i].to == f) continue;
getDis(edge[i].to, x, (d + edge[i].dis) % 3);
}
}
int cal(int x, int d){
cnt[0] = cnt[1] = cnt[2] = 0;
getDis(x, 0, d);
return cnt[0] * cnt[0] + cnt[1] * cnt[2] * 2;
}
int ans;
void solve(int x){
ans += cal(x, 0);
vis[x] = 1;
for(int i = head[x]; i; i = edge[i].nxt){
if(vis[edge[i].to]) continue;
ans -= cal(edge[i].to, edge[i].dis % 3);
root = 0, sum = size[edge[i].to], mxson[0] = INF;
findRoot(edge[i].to, 0);
solve(root);
}
}
int gcd(int a, int b){
return b == 0 ? a : gcd(b, a % b);
}
int main(){
scanf("%d", &n);
for(int i = 1; i < n; i++){
scanf("%d%d%d", &u, &v, &p);
addEdge(u, v, p % 3);
addEdge(v, u, p % 3);
}
root = 0, mxson[0] = INF, sum = n;
findRoot(1, 0);
solve(root);
int g = gcd(ans, n*n);
printf("%d/%d", ans / g, n * n / g);
return 0;
}
[IOI]Race
题意
给一棵树,每条边有权。求一条简单路径,权值和等于 K ,且边的数量最小。输出最小边数
题解
发现这道不能容斥…所以我们想办法通过子树信息直接计算经过分治点的路径的答案
记$tmp[i]$为当前子树中,路径长为$i$的最小边数,于是对于当前根$x$,我们每次遍历它的子树,先用$tmp[]$和正在遍历的子树更新答案(代码中的 $updAns()$ 函数),再用正在遍历的这颗子树更新$tmp[]$(代码中的 $updTmp()$ 函数),这样就保证了不会把不合法的路径算进来
Code1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
using namespace std;
const int INF = 1e9;
const int N = 200005;
int n, k, u, v, p;
struct Edge{
int nxt, to, dis;
}edge[N<<1];
int head[N], edgeNum;
void addEdge(int from, int to, int dis){
edge[++edgeNum].nxt = head[from];
edge[edgeNum].to = to;
edge[edgeNum].dis = dis;
head[from] = edgeNum;
}
int root, mxson[N], size[N], sum;
bool vis[N];
void findRoot(int x, int f){
size[x] = 1, mxson[x] = 0;
for(int i = head[x]; i; i = edge[i].nxt){
if(vis[edge[i].to] || edge[i].to == f) continue;
findRoot(edge[i].to, x);
size[x] += size[edge[i].to];
mxson[x] = max(mxson[x], size[edge[i].to]);
}
mxson[x] = max(mxson[x], sum - size[x]);
if(mxson[x] < mxson[root]) root = x;
}
int ans = INF, tmp[1000005];
void updTmp(int x, int f, int dis, int d){
if(dis <= k) tmp[dis] = min(tmp[dis], d);
for(int i = head[x]; i; i = edge[i].nxt){
if(vis[edge[i].to] || edge[i].to == f) continue;
updTmp(edge[i].to, x, dis + edge[i].dis, d + 1);
}
}
void updAns(int x, int f, int dis, int d){
if(dis <= k) ans = min(ans, d + tmp[k-dis]);
for(int i = head[x]; i; i = edge[i].nxt){
if(vis[edge[i].to] || edge[i].to == f) continue;
updAns(edge[i].to, x, dis + edge[i].dis, d + 1);
}
}
void clearTmp(int x, int f, int dis){
if(dis <= k) tmp[dis] = INF;
for(int i = head[x]; i; i = edge[i].nxt){
if(vis[edge[i].to] || edge[i].to == f) continue;
clearTmp(edge[i].to, x, dis + edge[i].dis);
}
}
void solve(int x){
vis[x] = 1, tmp[0] = 0;
for(int i = head[x]; i; i = edge[i].nxt){
if(vis[edge[i].to]) continue;
updAns(edge[i].to, x, edge[i].dis, 1);
updTmp(edge[i].to, x, edge[i].dis, 1);
}
for(int i = head[x]; i; i = edge[i].nxt){
if(vis[edge[i].to]) continue;
clearTmp(edge[i].to, x, edge[i].dis);
}
for(int i = head[x]; i; i = edge[i].nxt){
if(vis[edge[i].to]) continue;
root = 0, sum = size[edge[i].to];
findRoot(edge[i].to, 0);
solve(root);
}
}
int main(){
scanf("%d%d", &n, &k);
for(int i = 1; i < n; i++){
scanf("%d%d%d", &u, &v, &p);
addEdge(u+1, v+1, p);
addEdge(v+1, u+1, p);
}
for(int i = 0; i <= k; i++) tmp[i] = INF;
root = 0, mxson[0] = INF, sum = n;
findRoot(1, 0);
solve(root);
if(ans == INF) puts("-1");
else printf("%d\n", ans);
return 0;
}
—— 完 ——