普通平衡树/文艺平衡树/二逼平衡树

Posted on | In ,
普通平衡树/文艺平衡树/二逼平衡树

普通平衡树

题目链接：
luogu3369
bzoj3224

解题思路

平衡树模板题，我分别用了 [非旋Treap] 和 [Splay] AC了本题。

一、Splay

每个节点表示一个值，同时记录该点及其子树大小、该点表示的值的出现次数、左右儿子、父节点。

  • 插入：将x前驱旋至根，x后继旋至根的右儿子，那么根的左儿子的右儿子即为要插入的位置，如果此位置上无数，则新建一个节点；否则该位置的出现次数和大小加1。
    • 注意：为了避免找不到x前驱和后继，应事先插入一个值为-INF和值为INF的节点。
  • 删除：将x前驱旋至根，x后继旋至根的右儿子，那么根的左儿子的右儿子即为要删除的节点，如果此节点大小为1，直接删除；否则该位置的出现次数和大小减1。
  • 查x排名：将x旋至根，则x排名为根的左儿子大小+1
  • 查排名为x的数：从根向下查找，如果当前节点的左儿子大小+1=x，则返回当前节点的值；否则，如果当前节点的左儿子大小$\geq$x，则向其右儿子查找；否则，向其左儿子查找。
  • 求x前驱：从根向下查找，如果当前节点的值小于等于x，更新ans并向其右儿子查找；否则，向其左儿子查找。更新时，不断取max即可。
  • 求x后继：从根向下查找，如果当前节点的值大于等于x，更新ans并向其左儿子查找；否则，向其右儿子查找。更新时，不断取min即可。

时间复杂度：每次操作 $O(log_2n)$

Code#1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
#include<cstdio>
#include<algorithm>

using namespace std;

const int INF = 0x7fffffff;
const int N = 100005;
int n, opt, q;

int cnt = 0, root = 0;

struct Splay_tree{
    int fa, son[2], size, val, times;
}tr[N];

inline void pushup(int x){
    if(x){
        tr[x].size = tr[x].times;
        if(tr[x].son[0])	tr[x].size += tr[tr[x].son[0]].size;
        if(tr[x].son[1])	tr[x].size += tr[tr[x].son[1]].size;
    }
}

inline void rotate(int x, int kind){
    int y = tr[x].fa, z = tr[y].fa, A = tr[y].son[kind], B = tr[x].son[kind], C = tr[x].son[!kind];
    tr[x].son[kind] = y, tr[x].fa = z;
    tr[y].son[!kind] = B, tr[y].fa = x, tr[B].fa = y;
    tr[z].son[tr[z].son[1] == y] = x;
    pushup(y), pushup(x);
}

inline void splay(int x, int goal){
    if(x == goal)	return;
    while(tr[x].fa != goal){
        int y = tr[x].fa, z = tr[y].fa;
        int isrson1 = tr[y].son[1] == x, isrson2 = tr[z].son[1] == y;
        if(z == goal)	rotate(x, !isrson1);
        else{
            if(isrson1 == isrson2)	rotate(y, !isrson2);
            else	rotate(x, !isrson1);
            rotate(x, !isrson2);
        }
    }
    if(goal == 0)	root = x;
}

inline int select(int x){
    int now = root;
    while(now){
        if(tr[now].val == x)	break;
        else if(tr[now].val < x)	now = tr[now].son[1];
        else if(tr[now].val > x)	now = tr[now].son[0];
    }
    if(!now)	return -1;
    return now;
}

inline int getPre(int x){
    int now = root, ans = -INF;
    while(now){
        if(tr[now].val < x){
            ans = max(ans, tr[now].val);
            now = tr[now].son[1];
        }
        else	now = tr[now].son[0];
    }
    return ans;
}

inline int getSub(int x){
    int now = root, ans = INF;
    while(now){
        if(tr[now].val > x){
            ans = min(ans, tr[now].val);
            now = tr[now].son[0];
        }
        else	now = tr[now].son[1];
    }
    return ans;
}

inline int getRank(int x){
    int now = root, ans = 0;
    while(now){
        if(tr[now].val == x){
            ans += tr[tr[now].son[0]].size + 1;
            break;
        }
        else if(tr[now].val < x){
            ans += tr[tr[now].son[0]].size + tr[now].times;
            now = tr[now].son[1];
        }
        else	now = tr[now].son[0];
    }
    return ans - 1;
}

inline int newNode(int val, int f){
    ++cnt;
    tr[cnt].val = val;
    tr[cnt].fa = f;
    tr[cnt].son[0] = tr[cnt].son[1] = 0;
    tr[cnt].size = tr[cnt].times = 1;
    return cnt;
}

inline void insert(int x){
    splay(select(getPre(x)), 0);
    splay(select(getSub(x)), root);
    int t = tr[tr[root].son[1]].son[0];
    if(!t)
        tr[tr[root].son[1]].son[0] = newNode(x, tr[root].son[1]);
    else	tr[t].times++, tr[t].size++;
    pushup(tr[root].son[1]);
    pushup(root);
}

inline void del(int x){
    splay(select(getPre(x)), 0);
    splay(select(getSub(x)), root);
    int t = tr[tr[root].son[1]].son[0];
    if(!t || tr[t].times == 0)	return;
    tr[t].times--, tr[t].size--;
    if(tr[t].times == 0)	tr[tr[root].son[1]].son[0] = 0;
    pushup(tr[root].son[1]);
    pushup(root);
}

inline int findRank(int x){
    int now = root;
    while(now){
        if(tr[tr[now].son[0]].size + 1 <= x && x <= tr[tr[now].son[0]].size + tr[now].times)	break;
        else if(tr[tr[now].son[0]].size + 1 > x)
            now = tr[now].son[0];
        else if(tr[tr[now].son[0]].size + tr[now].times < x){
            x -= tr[tr[now].son[0]].size + tr[now].times;
            now = tr[now].son[1];
        }
    }
    return tr[now].val;
}

int main(){
    scanf("%d", &n);
    root = newNode(-INF, 0);
    tr[root].son[1] = newNode(INF, root), pushup(root);
    while(n--){
        scanf("%d%d", &opt, &q);
        if(opt == 1)	insert(q);
        else if(opt == 2)	del(q);
        else if(opt == 3)	printf("%d\n", getRank(q));
        else if(opt == 4)	printf("%d\n", findRank(q+1));
        else if(opt == 5)	printf("%d\n", getPre(q));
        else if(opt == 6)	printf("%d\n", getSub(q));
    }
    return 0;
}

二、非旋Treap

每个节点表示一个值，同时记录该点及其子树大小、左右儿子。

  • 插入：从x处split，新建一个值为x的节点，再将三部分merge起来。（注：从x处分开：x在前一部分，下同）
  • 删除：从x、x+1处split成三部分（记为l、t、r），将t的左右儿子merge起来，这样就删除了一个节点，再将三部分merge起来。
  • 查x排名：从x-1处split，则x排名为前一部分的大小+1
  • 查排名为x的数：同Splay
  • 求x前驱：同Splay
  • 求x后继：同Splay

时间复杂度：每次操作 $O(log_2n)$

Code#2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
#include<cstdio>
#include<algorithm>

using namespace std;

const int INF = 1e9;
const int N = 100005;
int n, opt, q;

struct Treap{
	int val, son[2], size, hp;
}tr[N];

struct OPT_Treap{
	int cnt, root;
	inline int newNode(int val){
		cnt++;
		tr[cnt].val = val;
		tr[cnt].hp = rand();
		tr[cnt].son[0] = tr[cnt].son[1] = 0;
		tr[cnt].size = 1;
		return cnt;
	}
	inline void pushup(int id){
		tr[id].size = 1;
		if(tr[id].son[0])	tr[id].size += tr[tr[id].son[0]].size;
		if(tr[id].son[1])	tr[id].size += tr[tr[id].son[1]].size;
	}
	inline void pushdown(int id){
		return;
	}
	int merge(int a, int b){
		if(a == 0)	return b;
		if(b == 0)	return a;
		if(tr[a].hp <= tr[b].hp){
			pushdown(a);
			tr[a].son[1] = merge(tr[a].son[1], b);
			pushup(a);
			return a;
		}
		else{
			pushdown(b);
			tr[b].son[0] = merge(a, tr[b].son[0]);
			pushup(b);
			return b;
		}
	}
	void split(int id, int k, int &x, int &y){
		if(!id){
			x = 0, y = 0;
			return;
		}
		pushdown(id);
		if(tr[id].val > k)
			y = id, split(tr[id].son[0], k, x, tr[id].son[0]);
		else
			x = id, split(tr[id].son[1], k, tr[id].son[1], y);
		pushup(id);
	}
	inline void insert(int val){
		int l = 0, r = 0;
		split(root, val, l, r);
		int t = newNode(val);
		root = merge(merge(l, t), r);
	}
	inline void del(int val){
		int l = 0, r = 0, t = 0;
		split(root, val - 1, l, t);
		split(t, val, t, r);
		t = merge(tr[t].son[0], tr[t].son[1]);
		root = merge(merge(l, t), r);
	}
	inline int getRank(int x){
		int ans = 0, l = 0, r = 0;
		split(root, x-1, l, r);
		ans = tr[l].size + 1;
		root = merge(l, r);
		return ans;
	}
	inline int getKth(int k){
		int now = root;
		while(now){
			if(tr[tr[now].son[0]].size + 1 == k)	return tr[now].val;
			else if(tr[tr[now].son[0]].size >= k)	now = tr[now].son[0];
			else	k -= (tr[tr[now].son[0]].size + 1), now = tr[now].son[1];
		}
		return -INF;
	}
	inline int getPre(int x){
		int ans = -INF, now = root;
		while(now){
			if(tr[now].val >= x)	now = tr[now].son[0];
			else{
				ans = max(ans, tr[now].val);
				now = tr[now].son[1];
			}
		}
		return ans;
	}
	inline int getSub(int x){
		int ans = INF, now = root;
		while(now){
			if(tr[now].val <= x)	now = tr[now].son[1];
			else{
				ans = min(ans, tr[now].val);
				now = tr[now].son[0];
			}
		}
		return ans;
	}
}BST;

int main(){
	srand(200127);
	scanf("%d", &n);
	BST.root = BST.newNode(INF);
	while(n--){
		scanf("%d%d", &opt, &q);
		if(opt == 1)	BST.insert(q);
		else if(opt == 2)	BST.del(q);
		else if(opt == 3)	printf("%d\n", BST.getRank(q));
		else if(opt == 4)	printf("%d\n", BST.getKth(q));
		else if(opt == 5)	printf("%d\n", BST.getPre(q));
		else if(opt == 6)	printf("%d\n", BST.getSub(q));
	}
	return 0;
}

文艺平衡树

题目链接：
luogu3391
bzoj3223

解题思路

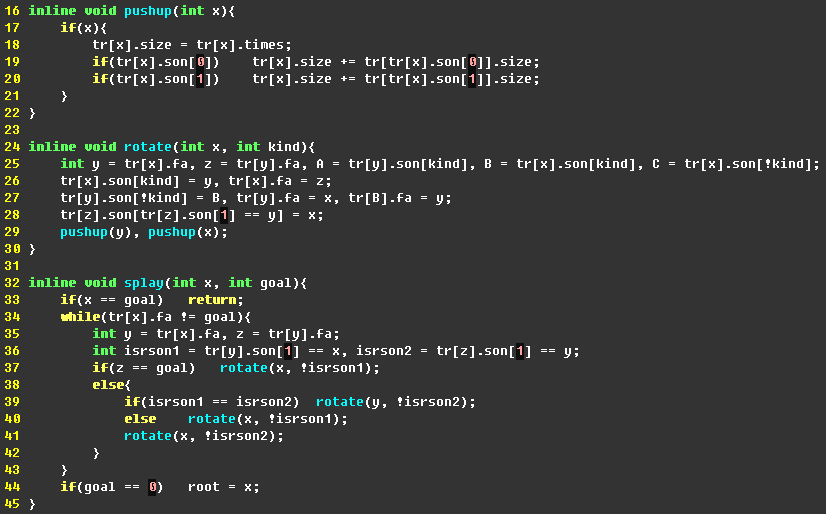
一、Splay

这道题只有区间翻转操作，线段树不好维护，只有用平衡树了。
对于一次$[l,r]$的区间翻转，把$l-1$旋至根，$r+1$旋至根的右儿子，那么$[l,r]$就在根的右儿子的左儿子处了。和线段树一样，我们可以将它的左右儿子互换后打上一个翻转标记(rev ^= 1)，之后再pushdown。

Code#3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
#include<cstdio>
#include<algorithm>

using namespace std;

const int INF = 0x7fffffff;
const int N = 100005;
int n, m, ql, qr;

int cnt, root;

struct Splay_tree{
    int fa, son[2], size, val;
    bool rev;
}tr[N];

inline void pushup(int x){
    if(x){
        tr[x].size = 1;
        if(tr[x].son[0])	tr[x].size += tr[tr[x].son[0]].size;
        if(tr[x].son[1])	tr[x].size += tr[tr[x].son[1]].size;
    }
}

inline void pushdown(int x){
    if(tr[x].rev){
        if(tr[x].son[0]){
            tr[tr[x].son[0]].rev ^= 1;
            swap(tr[tr[x].son[0]].son[0], tr[tr[x].son[0]].son[1]);
        }
        if(tr[x].son[1]){
            tr[tr[x].son[1]].rev ^= 1;
            swap(tr[tr[x].son[1]].son[0], tr[tr[x].son[1]].son[1]);
        }
        tr[x].rev = 0;
    }
}

inline void rotate(int x, int kind){
    int y = tr[x].fa, z = tr[y].fa, A = tr[y].son[kind], B = tr[x].son[kind], C = tr[x].son[!kind];
    tr[x].son[kind] = y, tr[x].fa = z;
    tr[y].son[!kind] = B, tr[y].fa = x;
    tr[z].son[tr[z].son[1] == y] = x;
    tr[B].fa = y;
    pushup(y), pushup(x);
}

inline void splay(int x, int goal){
    if(x == goal)	return;
    while(tr[x].fa != goal){
        int y = tr[x].fa, z = tr[y].fa;
        pushdown(z), pushdown(y), pushdown(x);
        int isrson1 = tr[y].son[1] == x, isrson2 = tr[z].son[1] == y;
        if(z == goal)	rotate(x, !isrson1);
        else{
            if(isrson1 == isrson2)	rotate(y, !isrson2);
            else	rotate(x, !isrson1);
            rotate(x, !isrson2);
        }
    }
    if(goal == 0)	root = x;
}

inline int newNode(int val, int f){
    cnt++;
    tr[cnt].val = val;
    tr[cnt].fa = f;
    tr[cnt].son[0] = tr[cnt].son[1] = 0;
    tr[cnt].size = 1;
    return cnt;
}

int select(int x){
    int now = root;
    pushdown(now);
    while(tr[tr[now].son[0]].size + 1 != x){
        if(tr[tr[now].son[0]].size + 1 > x)	now = tr[now].son[0];
        else{
            x -= tr[tr[now].son[0]].size + 1;
            now = tr[now].son[1];
        }
        pushdown(now);
    }
    return now;
}

inline void reverse(int l, int r){
    splay(select(l-1), 0);
    splay(select(r+1), root);
    int t = tr[tr[root].son[1]].son[0];
    tr[t].rev ^= 1;
    swap(tr[t].son[0], tr[t].son[1]);
}

int build(int l, int r, int f){
    if(l > r)	return 0;
    int mid = (l + r) >> 1, x = ++cnt;
    tr[x].val = mid - 1;
    tr[x].size = 1;
    tr[x].fa = f;
    tr[x].rev = 0;
    tr[x].son[0] = build(l, mid-1, x);
    tr[x].son[1] = build(mid+1, r, x);
    pushup(x);
    return x;
}

void print(int x){
    pushdown(x);
    if(tr[x].son[0])	print(tr[x].son[0]);
    if(tr[x].val >= 1 && tr[x].val <= n)	printf("%d ", tr[x].val);
    if(tr[x].son[1])	print(tr[x].son[1]);
}

int main(){
    scanf("%d%d", &n, &m);
    root = build(1, n+2, 0);
    while(m--){
        scanf("%d%d", &ql, &qr);
        reverse(ql+1, qr+1);
    }
    print(root);
    return 0;
}

二、非旋Treap

同上。

Code#4

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
#include<cstdio>
#include<algorithm>

using namespace std;

const int INF = 1e9;
const int N = 100005;
int n, m, ql, qr;

struct Treap{
	int val, size, son[2], hp;
	bool rev;
}tr[N];

struct OPT_Treap{
	int cnt, root;
	inline int newNode(int val){
		cnt++;
		tr[cnt].val = val;
		tr[cnt].hp = rand();
		tr[cnt].size = 1;
		tr[cnt].son[0] = tr[cnt].son[1] = 0;
		tr[cnt].rev = 0;
		return cnt;
	}
	inline void pushup(int id){
		if(!id)	return;
		tr[id].size = 1;
		if(tr[id].son[0])	tr[id].size += tr[tr[id].son[0]].size;
		if(tr[id].son[1])	tr[id].size += tr[tr[id].son[1]].size;
	}
	inline void pushdown(int id){
		if(!tr[id].rev)	return;
		if(tr[id].son[0]){
			int t = tr[id].son[0];
			tr[t].rev ^= 1;
			swap(tr[t].son[0], tr[t].son[1]);
		}
		if(tr[id].son[1]){
			int t = tr[id].son[1];
			tr[t].rev ^= 1;
			swap(tr[t].son[0], tr[t].son[1]);
		}
		tr[id].rev ^= 1;
	}
	int merge(int a, int b){
		if(a == 0)	return b;
		if(b == 0)	return a;
		if(tr[a].hp <= tr[b].hp){
			pushdown(a);
			tr[a].son[1] = merge(tr[a].son[1], b);
			pushup(a);
			return a;
		}
		else{
			pushdown(b);
			tr[b].son[0] = merge(a, tr[b].son[0]);
			pushup(b);
			return b;
		}
	}
	void split(int id, int k, int &x, int &y){
		if(!id){
			x = 0, y = 0;
			return;
		}
		pushdown(id);
		if(tr[tr[id].son[0]].size >= k)
			y = id, split(tr[id].son[0], k, x, tr[id].son[0]);
		else
			x = id, split(tr[id].son[1], k - tr[tr[id].son[0]].size - 1, tr[id].son[1], y);
		pushup(id);
	}
	inline void reverse(int l, int r){
		int L, t, R;
		split(root, l - 1, L, t);
		split(t, r - l + 1, t, R);
		tr[t].rev ^= 1;
		swap(tr[t].son[0], tr[t].son[1]);
		root = merge(merge(L, t), R);
	}
	inline int build(int l, int r){
		if(l > r)	return 0;
		int mid = (l + r) >> 1;
		int t = newNode(mid);
		tr[t].son[0] = build(l, mid - 1);
		tr[t].son[1] = build(mid + 1, r);
		pushup(t);
		return t;
	}
}BST;

void print(int x){
	BST.pushdown(x);
	if(tr[x].son[0])	print(tr[x].son[0]);
	printf("%d ", tr[x].val);
	if(tr[x].son[1])	print(tr[x].son[1]);
}

int main(){
	srand(200127);
	scanf("%d%d", &n, &m);
	BST.root = BST.build(1, n);
	while(m--){
		scanf("%d%d", &ql, &qr);
		BST.reverse(ql, qr);
	}
	print(BST.root);
	return 0;
}

二逼平衡树

题目链接：
luogu3380
bzoj3196

解题思路

一、线段树套Splay

这道题与普通平衡树唯一的不同就在于所有查询都是区间查询，那么我们需要在平衡树外面套一层线段树以供区间查询，即线段树套平衡树。
当然，并非真的要在每个线段树节点内建一颗平衡树，存一下在这个节点的平衡树的根的编号就行了。

  • 查询区间内k的排名：在线段树上递归找查询的区间，在相应节点上的平衡树上查询比k小的数的个数，回溯时将所有答案相加得到了区间内比k小的数的个数，最后+1就是排名；
  • 查询区间内排名为k的值：这个要麻烦一点，由于不同线段树节点上的答案不能进行合并，只能考虑二分答案，问题转化为二分出的答案在区间内的排名问题，即第一问；
  • 修改某位置的值：修改即先删除原值，再插入新值；在线段树上找到该节点，对所经路线上所有线段树里的平衡树进行删除插入操作；
  • 查询k在区间内的前驱：同第一问，只不过在更新答案时不是相加，而是取max；
  • 查询k在区间内的后继：同第一问，只不过在更新答案时不是相加，而是取min。

Code#5

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
#include<cstdio>
#include<iostream>
#include<algorithm>

#define lid id<<1
#define rid id<<1|1
#define mid ((A[id].l+A[id].r)>>1)

using namespace std;

const int INF = 0x7fffffff;
const int N = 50005;
int n, m, a[N], opt, ql, qr, qk, qpos, tmp;

struct splay{
    int size, times, val, son[2], fa;
}B[(int)4e6];

struct segTree{
    int l, r, root;
}A[N<<2];

struct OPT_splay{
    int cnt;
    inline void pushup(int x){
        if(x){
            B[x].size = B[x].times;
            if(B[x].son[0])	B[x].size += B[B[x].son[0]].size;
            if(B[x].son[1])	B[x].size += B[B[x].son[1]].size;
        }
    }
    inline void rotate(int x, int kind){
        int y = B[x].fa, z = B[y].fa, a = B[y].son[kind], b = B[x].son[kind], c = B[x].son[!kind];
        B[x].fa = z, B[x].son[kind] = y;
        B[y].fa = x, B[y].son[!kind] = b;
        B[z].son[B[z].son[1] == y] = x;
        B[b].fa = y;
        pushup(y), pushup(x);
    }
    inline void splay(int x, int goal, int id){
        if(x == goal)	return;
        while(B[x].fa != goal){
            int y = B[x].fa, z = B[y].fa;
            int isrson1 = B[y].son[1] == x, isrson2 = B[z].son[1] == y;
            if(z == goal)	rotate(x, !isrson1);
            else{
                if(isrson1 == isrson2)	rotate(y, !isrson2);
                else	rotate(x, !isrson1);
                rotate(x, !isrson2);
            }
        }
        if(goal == 0)	A[id].root = x;
    }
    inline int newNode(int val, int fa){
        cnt++;
        B[cnt].fa = fa;
        B[cnt].val = val;
        B[cnt].size = B[cnt].times = 1;
        B[cnt].son[0] = B[cnt].son[1] = 0;
        return cnt;
    }
    inline int getPre(int x, int id){
        int now = A[id].root, res = -INF;
        while(now){
            if(B[now].val < x){
                res = max(res, B[now].val);
                now = B[now].son[1];
            }
            else	now = B[now].son[0];
        }
        return res;
    }
    inline int getSub(int x, int id){
        int now = A[id].root, res = INF;
        while(now){
            if(B[now].val > x){
                res = min(res, B[now].val);
                now = B[now].son[0];
            }
            else	now = B[now].son[1];
        }
        return res;
    }
    inline int select(int x, int id){
        int now = A[id].root;
        while(now){
            if(B[now].val == x)	break;
            else if(B[now].val > x)	now = B[now].son[0];
            else if(B[now].val < x)	now = B[now].son[1];
        }
        if(!now)	return -1;
        return now;
    }
    inline int getRank(int x, int id){
        if(select(x, id) != -1)	splay(select(x, id), 0, id);
        else	splay(select(getSub(x, id), id), 0, id);
        return B[B[A[id].root].son[0]].size;
    }
    inline void insert(int val, int id){
        splay(select(getPre(val, id), id), 0, id);
        splay(select(getSub(val, id), id), A[id].root, id);
        int t = B[B[A[id].root].son[1]].son[0];
        if(!t)	B[B[A[id].root].son[1]].son[0] = newNode(val, B[A[id].root].son[1]);
        else	B[t].times++, B[t].size++;
        pushup(B[A[id].root].son[1]);
        pushup(A[id].root);
    }
    inline void del(int val, int id){
        splay(select(getPre(val, id), id), 0, id);
        splay(select(getSub(val, id), id), A[id].root, id);
        int t = B[B[A[id].root].son[1]].son[0];
        if(!t || B[t].times == 0)	return;
        B[t].times--, B[t].size--;
        if(B[t].times == 0)	B[B[A[id].root].son[1]].son[0] = 0;
        pushup(B[A[id].root].son[1]);
        pushup(A[id].root);
    }
}Splay;

struct OPT_segTree{
    void build(int id, int l, int r){
        A[id].root = Splay.newNode(-INF, 0);
        B[A[id].root].son[1] = Splay.newNode(INF, A[id].root);
        A[id].l = l, A[id].r = r;
        if(A[id].l == A[id].r)	return;
        build(lid, l, mid);
        build(rid, mid+1, r);
    }
    void insert(int id, int pos, int val){
        Splay.insert(val, id);
        if(A[id].l == A[id].r)	return;
        if(pos <= mid)	insert(lid, pos, val);
        else	insert(rid, pos, val);
    }
    int getRank(int id, int l, int r, int x){
        if(A[id].l == l && A[id].r == r)	return Splay.getRank(x, id) - 1;
        if(r <= mid)	return getRank(lid, l, r, x);
        else if(l > mid)	return getRank(rid, l, r, x);
        else	return getRank(lid, l, mid, x) + getRank(rid, mid+1, r, x);
    }
    int getKth(int l, int r, int k){
        int ans = -1, L = 0, R = 1e8;
        while(L <= R){
            int Mid = (L + R) >> 1;
            int t1 = getRank(1, l, r, Mid) + 1;
            int t2 = getRank(1, l, r, Mid+1);
            if(t1 <= k && k <= t2){ ans = Mid; break; }
            if(t2 < k)	L = Mid+1;
            else if(t1 > k)	R = Mid-1;
        }
        return ans;
    }
    void modify(int id, int pos, int val){
        Splay.del(a[pos], id);
        Splay.insert(val, id);
        if(A[id].l == A[id].r)	return;
        if(pos <= mid)	modify(lid, pos, val);
        else	modify(rid, pos, val);
    }
    int getPre(int id, int l, int r, int x){
        if(A[id].l == l && A[id].r == r)	return Splay.getPre(x, id);
        if(r <= mid)	return getPre(lid, l, r, x);
        else if(l > mid)	return getPre(rid, l, r, x);
        else	return max(getPre(lid, l, mid, x), getPre(rid, mid+1, r, x));
    }
    int getSub(int id, int l, int r, int x){
        if(A[id].l == l && A[id].r == r)	return Splay.getSub(x, id);
        if(r <= mid)	return getSub(lid, l, r, x);
        else if(l > mid)	return getSub(rid, l, r, x);
        else	return min(getSub(lid, l, mid, x), getSub(rid, mid+1, r, x));
    }
}Seg;

int main(){
    scanf("%d%d", &n, &m);
    Seg.build(1, 1, n);
    for(int i = 1; i <= n; i++){
        scanf("%d", &a[i]);
        Seg.insert(1, i, a[i]);
    }
    while(m--){
        scanf("%d", &opt);
        if(opt == 3)	scanf("%d%d", &qpos, &qk);
        else	scanf("%d%d%d", &ql, &qr, &qk);
        if(opt == 1)	printf("%d\n", Seg.getRank(1, ql, qr, qk) + 1);
        else if(opt == 2)	printf("%d\n", Seg.getKth(ql, qr, qk));
        else if(opt == 3)	Seg.modify(1, qpos, qk), a[qpos] = qk;
        else if(opt == 4)	printf("%d\n", Seg.getPre(1, ql, qr, qk));
        else if(opt == 5)	printf("%d\n", Seg.getSub(1, ql, qr, qk));
    }
    return 0;
}

二、线段树套非旋Treap

同上。

Code#6

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
#include<cstdio>
#include<algorithm>

#define lid id<<1
#define rid id<<1|1
#define mid ((A[id].l + A[id].r) >> 1)

using namespace std;

const int INF = 0x7fffffff;
const int N = 50005;
int n, m, opt, ql, qr, qk, qpos, a[N];

struct Treap{
	int val, son[2], size, hp;
}B[(int)4e6];
struct segTree{
	int l, r, root;
}A[N<<2];

struct OPT_Treap{
	int cnt;
	inline int newNode(int val){
		cnt++;
		B[cnt].val = val;
		B[cnt].son[0] = B[cnt].son[1] = 0;
		B[cnt].size = 1;
		B[cnt].hp = rand();
		return cnt;
	}
	inline void pushup(int id){
		if(!id)	return;
		B[id].size = 1;
		if(B[id].son[0])	B[id].size += B[B[id].son[0]].size;
		if(B[id].son[1])	B[id].size += B[B[id].son[1]].size;
	}
	int merge(int a, int b){
		if(a == 0)	return b;
		if(b == 0)	return a;
		if(B[a].hp <= B[b].hp){
			B[a].son[1] = merge(B[a].son[1], b);
			pushup(a);
			return a;
		}
		else{
			B[b].son[0] = merge(a, B[b].son[0]);
			pushup(b);
			return b;
		}
	}
	void split(int id, int k, int &x, int &y){
		if(!id){
			x = 0, y = 0;
			return;
		}
		if(B[id].val > k)
			y = id, split(B[id].son[0], k, x, B[id].son[0]);
		else
			x = id, split(B[id].son[1], k, B[id].son[1], y);
		pushup(id);
	}
	inline void insert(int &rt, int val){
		int l = 0, r = 0;
		split(rt, val, l, r);
		int t = newNode(val);
		rt = merge(merge(l, t), r);
	}
	inline void del(int &rt, int val){
		int l = 0, r = 0, t = 0;
		split(rt, val - 1, l, t);
		split(t, val, t, r);
		t = merge(B[t].son[0], B[t].son[1]);
		rt = merge(merge(l, t), r);
	}
	inline int getRank(int &rt, int x){
		int l = 0, r = 0;
		split(rt, x - 1, l, r);
		int ans = B[l].size + 1;
		rt = merge(l, r);
		return ans;
	}
	inline int getPre(int &rt, int x){
		int now = rt, ans = -INF;
		while(now){
			if(B[now].val < x){
				ans = max(ans, B[now].val);
				now = B[now].son[1];
			}
			else	now = B[now].son[0];
		}
		return ans;
	}
	inline int getSub(int &rt, int x){
		int now = rt, ans = INF;
		while(now){
			if(B[now].val > x){
				ans = min(ans, B[now].val);
				now = B[now].son[0];
			}
			else	now = B[now].son[1];
		}
		return ans;
	}
}BST;

struct OPT_segTree{
	void build(int id, int l, int r){
		A[id].l = l, A[id].r = r;
		A[id].root = BST.newNode(INF);
		if(A[id].l == A[id].r)	return;
		build(lid, l, mid);
		build(rid, mid+1, r);
	}
	void insert(int id, int pos, int val){
		BST.insert(A[id].root, val);
		if(A[id].l == A[id].r)	return;
		if(pos <= mid)	insert(lid, pos, val);
		else	insert(rid, pos, val);
	}
	void modify(int id, int pos, int val){
		BST.del(A[id].root, a[pos]);
		BST.insert(A[id].root, val);
		if(A[id].l == A[id].r)	return;
		if(pos <= mid)	modify(lid, pos, val);
		else	modify(rid, pos, val);
	}
	int query(int id, int l, int r, int x, int kind){
		if(A[id].l == l && A[id].r == r){
			if(kind == 0)	return BST.getRank(A[id].root, x);
			if(kind == 1)	return BST.getPre(A[id].root, x);
			if(kind == 2)	return BST.getSub(A[id].root, x);
		}
		if(r <= mid)	return query(lid, l, r, x, kind);
		else if(l > mid)	return query(rid, l, r, x, kind);
		else{
			if(kind == 0)	return query(lid, l, mid, x, kind) + query(rid, mid+1, r, x, kind) - 1;
			if(kind == 1)	return max(query(lid, l, mid, x, kind), query(rid, mid+1, r, x, kind));
			if(kind == 2)	return min(query(lid, l, mid, x, kind), query(rid, mid+1, r, x, kind));
		}
	}
	int getKth(int l, int r, int k){
		int L = 0, R = 1e8, ans = 0;
		while(L <= R){
			int Mid = (L + R) >> 1;
			int t1 = query(1, l, r, Mid, 0);
			int t2 = query(1, l, r, Mid+1, 0) - 1;
			if(t1 <= k && k <= t2){ ans = Mid; break; }
			else if(t2 < k)	L = Mid + 1;
			else if(t1 > k)	R = Mid - 1;
		}
		return ans;
	}
}Seg;

int main(){
	srand(200127);
	scanf("%d%d", &n, &m);
	BST.cnt = 0;
	Seg.build(1, 1, n);
	for(int i = 1; i <= n; i++){
		scanf("%d", &a[i]);
		Seg.insert(1, i, a[i]);
	}
	while(m--){
		scanf("%d", &opt);
		if(opt == 3)	scanf("%d%d", &qpos, &qk);
		else	scanf("%d%d%d", &ql, &qr, &qk);
		if(opt == 1)	printf("%d\n", Seg.query(1, ql, qr, qk, 0));
		else if(opt == 2)	printf("%d\n", Seg.getKth(ql, qr, qk));
		else if(opt == 3)	Seg.modify(1, qpos, qk), a[qpos] = qk;
		else if(opt == 4)	printf("%d\n", Seg.query(1, ql, qr, qk, 1));
		else if(opt == 5)	printf("%d\n", Seg.query(1, ql, qr, qk, 2));
	}
	return 0;
}

三、树状数组套值域线段树（带修改主席树）

hmm…这道题其实可以不用平衡树做，因为要求第k大，自然而然想到主席树可以做到，但这道题有修改操作，普通的维护前缀和的主席树修改一次就要把后面所有树都改了，所以修改一次的时间复杂度就是$O(NlogN)$的，显然不行。于是，带修改主席树应运而生：我们不再让值域线段树们维护前缀和了，而是让它们维护树状数组上对应的约$logN$个点，这样一次修改的时间复杂度就降到了$O(log_2^2N)$。

  • 查询区间内k的排名：相当于找比k小的数有多少个（答案是个数+1）。在值域线段树上二分查找k时，如果往右儿子走，就把左儿子大小加进答案里去就行了；
  • 查询区间内排名为k的值：找到树状数组里面相关的值域线段树（存进一个数组，见代码中的A[]和B[]），算出当前点左儿子大小，再决定是向左还是向右二分下去；
  • 修改某位置的值：修改即先删除原值，再插入新值；找到树状数组里面相关的值域线段树，对每棵树都进行删除和插入操作；
  • 查询k在区间内的前驱：查询区间内比k小的数有多少个，如果没有，输出-INF；否则输出区间内相应排名的值；
  • 查询k在区间内的后继：查询区间内比k大的数有多少个，如果没有，输出INF；否则输出区间内相应排名的值。

涉及到值域线段树一般都要离散化，以保证空间；同时，这道题还必须动态开点才能保证空间。

Code#7

纪念我的第一份超过200行的代码…

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
#include<cstdio>
#include<algorithm>

using namespace std;

const int INF = 0x7fffffff;
const int N = 50005;
int n, m, a[N], t[N<<1], f[N<<1], MX, A[20], B[20];//因为有询问操作，t[]和f[]空间一定要开够!
int root[N], cnt;

struct Query{
	int opt, l, r, k, pos;
}q[N];

struct segTree{
	int size, son[2];
}tr[N*15*15];

inline void readin(){
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= n; i++)	scanf("%d", &a[i]), t[++t[0]] = a[i];
	for(int i = 1; i <= m; i++){
		scanf("%d", &q[i].opt);
		if(q[i].opt != 3){
			scanf("%d%d%d", &q[i].l, &q[i].r, &q[i].k);
			if(q[i].opt != 2)	t[++t[0]] = q[i].k;
		}
		else{
			scanf("%d%d", &q[i].pos, &q[i].k);
			t[++t[0]] = q[i].k;
		}
	}
}
inline void disc(){
	sort(t+1, t+t[0]+1);
	int len = unique(t+1, t+t[0]+1) - (t+1);
	for(int i = 1; i <= n; i++){
		int temp = lower_bound(t+1, t+len+1, a[i]) - t;
		f[temp] = a[i], a[i] = temp;
		MX = max(MX, temp);
	}
	for(int i = 1; i <= m; i++){
		if(q[i].opt == 2)	continue;
		int temp = lower_bound(t+1, t+len+1, q[i].k) - t;
		f[temp] = q[i].k, q[i].k = temp;
		MX = max(MX, temp);
	}
	f[MX+1] = -INF;
	f[MX+2] = INF;
}
inline int lowbit(int x){ return x & -x; }

inline void init1(int x, int X[]){
	X[0] = 0;
	for(int i = x; i; i -= lowbit(i)){
		if(!root[i])	root[i] = ++cnt;
		X[++X[0]] = root[i];
	}
}
inline void init2(int x, int X[]){
	X[0] = 0;
	for(int i = x; i <= n; i += lowbit(i)){
		if(!root[i])	root[i] = ++cnt;
		X[++X[0]] = root[i];
	}
}

inline void pushup(int id){
	tr[id].size = tr[tr[id].son[0]].size + tr[tr[id].son[1]].size;
}

void insert(int &id, int l, int r, int val){
	if(!id)	id = ++cnt;
	if(l == r){
		tr[id].size++;
		return;
	}
	int mid = (l + r) >> 1;
	if(val <= mid)	insert(tr[id].son[0], l, mid, val);
	else	insert(tr[id].son[1], mid+1, r, val);
	pushup(id);
}

void del(int &id, int l, int r, int val){
	if(!id)	id = ++cnt;
	if(l == r){
		if(tr[id].size > 0)	tr[id].size--;
		return;
	}
	int mid = (l + r) >> 1;
	if(val <= mid)	del(tr[id].son[0], l, mid, val);
	else	del(tr[id].son[1], mid+1, r, val);
	pushup(id);
}

int getSmaller(int l, int r, int k){
	if(l == r)	return 0;
	int mid = (l + r) >> 1;
	if(k <= mid){
		for(int i = 1; i <= A[0]; i++){
			if(!tr[A[i]].son[0])	tr[A[i]].son[0] = ++cnt;
			A[i] = tr[A[i]].son[0];
		}
		for(int i = 1; i <= B[0]; i++){
			if(!tr[B[i]].son[0])	tr[B[i]].son[0] = ++cnt;
			B[i] = tr[B[i]].son[0];
		}
		return getSmaller(l, mid, k);
	}
	else{
		int res = 0;
		for(int i = 1; i <= A[0]; i++){
			if(!tr[A[i]].son[1])	tr[A[i]].son[1] = ++cnt;
			res -= tr[tr[A[i]].son[0]].size;
			A[i] = tr[A[i]].son[1];
		}
		for(int i = 1; i <= B[0]; i++){
			if(!tr[B[i]].son[1])	tr[B[i]].son[1] = ++cnt;
			res += tr[tr[B[i]].son[0]].size;
			B[i] = tr[B[i]].son[1];
		}
		return res + getSmaller(mid+1, r, k);
	}
}

int getBigger(int l, int r, int k){
	if(l == r)	return 0;
	int mid = (l + r) >> 1;
	if(k <= mid){
		int res = 0;
		for(int i = 1; i <= A[0]; i++){
			if(!tr[A[i]].son[0])	tr[A[i]].son[0] = ++cnt;
			res -= tr[tr[A[i]].son[1]].size;
			A[i] = tr[A[i]].son[0];
		}
		for(int i = 1; i <= B[0]; i++){
			if(!tr[B[i]].son[0])	tr[B[i]].son[0] = ++cnt;
			res += tr[tr[B[i]].son[1]].size;
			B[i] = tr[B[i]].son[0];
		}
		return res + getBigger(l, mid, k);
	}
	else{
		for(int i = 1; i <= A[0]; i++){
			if(!tr[A[i]].son[1])	tr[A[i]].son[1] = ++cnt;
			A[i] = tr[A[i]].son[1];
		}
		for(int i = 1; i <= B[0]; i++){
			if(!tr[B[i]].son[1])	tr[B[i]].son[1] = ++cnt;
			B[i] = tr[B[i]].son[1];
		}
		return getBigger(mid+1, r, k);
	}
}

int getKth(int l, int r, int k){
	if(l == r)	return l;
	int lsize = 0;
	for(int i = 1; i <= A[0]; i++)	lsize -= tr[tr[A[i]].son[0]].size;
	for(int i = 1; i <= B[0]; i++)	lsize += tr[tr[B[i]].son[0]].size;
	int mid = (l + r) >> 1;
	if(lsize >= k){
		for(int i = 1; i <= A[0]; i++){
			if(!tr[A[i]].son[0])	tr[A[i]].son[0] = ++cnt;
			A[i] = tr[A[i]].son[0];
		}
		for(int i = 1; i <= B[0]; i++){
			if(!tr[B[i]].son[0])	tr[B[i]].son[0] = ++cnt;
			B[i] = tr[B[i]].son[0];
		}
		return getKth(l, mid, k);
	}
	else{
		for(int i = 1; i <= A[0]; i++){
			if(!tr[A[i]].son[1])	tr[A[i]].son[1] = ++cnt;
			A[i] = tr[A[i]].son[1];
		}
		for(int i = 1; i <= B[0]; i++){
			if(!tr[B[i]].son[1])	tr[B[i]].son[1] = ++cnt;
			B[i] = tr[B[i]].son[1];
		}
		return getKth(mid+1, r, k - lsize);
	}
}

inline int getPre(int ql, int qr, int k){
	init1(ql-1, A), init1(qr, B);
	int rank = getSmaller(1, MX, k) + 1;
	init1(ql-1, A), init1(qr, B);
	if(rank == 1)	return MX+1;
	else	return getKth(1, MX, rank-1);
}

inline int getSub(int ql, int qr, int k){
	init1(ql-1, A), init1(qr, B);
	int rank = getBigger(1, MX, k) + 1;
	init1(ql-1, A), init1(qr, B);
	if(rank == 1)	return MX+2;
	else	return getKth(1, MX, qr - ql + 3 - rank);
}

int main(){
	readin();
	disc();
	for(int i = 1; i <= n; i++){
		init2(i, A);
		for(int j = 1; j <= A[0]; j++)
			insert(A[j], 1, MX, a[i]);
	}
	for(int i = 1; i <= m; i++){
		switch(q[i].opt){
			case 1: init1(q[i].l-1, A); init1(q[i].r, B); printf("%d\n", getSmaller(1, MX, q[i].k) + 1); break;
			case 2: init1(q[i].l-1, A); init1(q[i].r, B); printf("%d\n", f[getKth(1, MX, q[i].k)]); break;
			case 3:{
				init2(q[i].pos, A);
				for(int j = 1; j <= A[0]; j++){
					del(A[j], 1, MX, a[q[i].pos]);
					insert(A[j], 1, MX, q[i].k);
				}
				a[q[i].pos] = q[i].k;
				break;
			}
			case 4: printf("%d\n", f[getPre(q[i].l, q[i].r, q[i].k)]); break;
			case 5: printf("%d\n", f[getSub(q[i].l, q[i].r, q[i].k)]); break;
		}
	}
	return 0;
}